Jackal 投稿日:2005/09/05(Mon)
お久しぶりです。
十三不搭を解いたので書き込みをしたいと思います。
まず赤牌等、同じ種類のもので違う扱いをするものは無いとします。一種の数牌において不搭子(というのか判りませんが搭子で無い物のこと)の組み合わせは、
(1)(2)(3)(4)(5)(6)(7)(8)(9)
(14)(15)(16)(17)(18)(19)
(25)(26)(27)(28)(29)
(36)(37)(38)(39)
(47)(48)(49)
(58)(59)
(69)
(147)(148)(149)(158)(159)(169)
(258)(259)(269)
(369)
になります。
よって、数牌1種につき組み合わせの数は
1枚の時:9種
2枚の時:21種
3枚の時:10種
となります。
ここで、字牌と数牌の組み合わせは
(字牌,数牌A,数牌B,数牌C)で、数牌の個数はA≧B≧Cとした時、
(7,3,3,0)
(7,3,2,1)
(7,2,2,2)
(6,3,3,1)
(6,3,2,2)
(5,3,3,2)
(4,3,3,3)
となります。
上から順に計算すると、
C(3,1)*10*10=300
C(3,1)*C(2,1)*10*21*9=6*1890=11340
21*21*21=(20+1)^3=20^3+3*20^2+3*20+1=8000+1200+60+1=9261
C(7,1)*C(3,1)*10*10*9=7*3*900=18900
C(7,1)*C(3,1)*10*21*21=92610
C(7,2)*C(3,1)*10*10*21=21^2*10^2*3=441*3*100=132300
C(7,3)*10*10*10=35000
となり、各々を足して、雀頭の選択のため13を掛けると899,133になります。これでいかがでしょうか。
|
の対子(トイツ)が一組あるだけで、あとはバラバラ。といっても
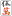
の嵌張(カンチャン)なんかがあるので、十三不搭にもならない。(゚0゚)